| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 12 Heron's Formula
Welcome to this dedicated resource offering comprehensive solutions for the NCERT Exemplar problems tailored for Class 9 students, focusing entirely on the application of Heron's Formula. The Exemplar questions are specifically designed to push your understanding beyond basic applications, presenting challenges that involve more complex calculations, the clever application of the formula to find areas of quadrilaterals through subdivision, and intricate word problems that demand a practical translation of real-world scenarios into geometric area calculations. This page aims to equip you with the methods and confidence needed to tackle these advanced problems effectively.
At the heart of this chapter lies Heron's Formula, a remarkable tool in geometry that allows us to calculate the area of a triangle when only the lengths of its three sides are known, without needing to know any angles or the height. The formula is elegantly expressed as: Area $= \sqrt{s(s-a)(s-b)(s-c)}$ Here, $a, b,$ and $c$ represent the lengths of the three sides of the triangle. The term $s$ is the semi-perimeter of the triangle, calculated simply as half the sum of the side lengths: $s = \frac{a+b+c}{2}$. Our solutions meticulously demonstrate the application of this formula to find the area of various types of triangles, including scalene, isosceles, and even equilateral triangles (though simpler formulas exist for the latter, Heron's still applies). You'll find examples where side lengths are given directly, situations involving variable side lengths, or cases where the third side must first be determined using given perimeter information.
A significant emphasis within the NCERT Exemplar problems, and consequently within these solutions, is placed on calculating the area of quadrilaterals and other polygons. Since Heron's formula applies directly only to triangles, the strategy involves dividing the polygon into constituent triangles using one or more diagonals. The key steps, clearly illustrated in the solutions, are:
- Strategically choosing and drawing a suitable diagonal (or diagonals) to partition the polygon into triangles.
- Ensuring the side lengths of these resulting triangles are known (either given directly or calculable, perhaps including the diagonal's length).
- Applying Heron's Formula individually to calculate the area of each triangle.
- Summing the areas of these triangles to find the total area of the original polygon.
Furthermore, the practical relevance of Heron's Formula is highlighted through various word problems. These often describe scenarios involving calculating the area of irregularly shaped fields, plots of land, or other planar figures encountered in real life. The challenge lies in extracting the necessary side lengths from the problem's description and applying the formula correctly. Some problems might extend this by asking for calculations related to cost, such as the cost of leveling a field or buying fertilizer, often quoted per unit area (e.g., at $\textsf{₹}50$ per square meter), requiring the calculated area as an intermediate step.
The solutions provided cover the full spectrum of Exemplar question types: Multiple Choice Questions (MCQs) testing formula comprehension or straightforward calculations, Fill-in-the-Blanks, True/False statements checking understanding of applicability and properties, and detailed Short/Long Answer questions. For these longer problems, the solutions offer meticulous step-by-step calculations, clearly showing the computation of the semi-perimeter ($s$) followed by the area calculation using the formula. Careful attention is given to handling square roots (simplification where possible or appropriate approximation) and presenting a logical flow for finding areas of composite shapes or solving complex word problems. This resource is designed to ensure you can apply Heron's formula accurately and confidently across diverse and demanding geometric situations.
Sample Question 1 (Before Exercise 12.1)
Write the correct answer:
Sample Question 1: The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be
(A) 24 cm2
(B) 40 cm2
(C) 48 cm2
(D) 80 cm2
Answer:
Given: A right triangle with:
- Base = 8 cm
- Hypotenuse = 10 cm
To Find: The area of the right triangle.
Solution: Let the right triangle be ABC, with the right angle at one vertex, say B. Let the base BC = 8 cm and the hypotenuse AC = 10 cm. We need to find the height AB.
According to the Pythagorean theorem in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
$\text{AB}^2 + \text{BC}^2 = \text{AC}^2$
... (i)
Substitute the given values into equation (i):
$\text{AB}^2 + (8 \text{ cm})^2 = (10 \text{ cm})^2$
$\text{AB}^2 + 64 \text{ cm}^2 = 100 \text{ cm}^2$
Subtract 64 cm$^2$ from both sides:
$\text{AB}^2 = 100 \text{ cm}^2 - 64 \text{ cm}^2$
$\text{AB}^2 = 36 \text{ cm}^2$
Take the square root of both sides:
$\text{AB} = \sqrt{36 \text{ cm}^2}$
$\text{AB} = 6 \text{ cm}$
(Length must be positive)
Now we have the base (BC = 8 cm) and the height (AB = 6 cm) of the right triangle.
The area of a triangle is given by the formula:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Substitute the values of BC and AB:
Area $= \frac{1}{2} \times 8 \text{ cm} \times 6 \text{ cm}$
Area $= \frac{1}{2} \times 48 \text{ cm}^2$
Area $= 24 \text{ cm}^2$
Comparing this result with the given options, we find that the area is 24 cm$^2$.
The correct option is (A) 24 cm2.
Exercise 12.1
Question 1. An isosceles right triangle has area 8 cm2 . The length of its hypotenuse is
(A) $\sqrt{32}$ cm
(B) $\sqrt{16}$ cm
(C) $\sqrt{48}$ cm
(D) $\sqrt{24}$ cm
Answer:
Given: An isosceles right triangle with Area = 8 cm$^2$.
To Find: The length of its hypotenuse.
Solution: Let the isosceles right triangle be ABC, with the right angle at B ($\angle\text{B} = 90^\circ$). In an isosceles right triangle, the two legs (the sides forming the right angle) are equal in length. Let the length of each leg be $x$ cm. So, AB = BC = $x$ cm.
The area of a right triangle is calculated as half the product of its legs.
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Here, we can take one leg as the base and the other leg as the height.
Area $= \frac{1}{2} \times \text{AB} \times \text{BC}$
Substitute the given area and the side lengths:
8 $\text{ cm}^2 = \frac{1}{2} \times x \text{ cm} \times x \text{ cm}$
8 $= \frac{1}{2} x^2$
Multiply both sides by 2 to solve for $x^2$:
$16 = x^2$
Now, find the value of $x$ by taking the square root:
$x = \sqrt{16}$
$x = 4$
(Length must be positive)
So, the length of each leg is 4 cm (AB = 4 cm and BC = 4 cm).
Now, we need to find the length of the hypotenuse AC. We can use the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
$\text{AC}^2 = \text{AB}^2 + \text{BC}^2$
... (i)
Substitute the values of AB and BC:
(Length must be positive)
Now, compare this result with the given options:
(A) $\sqrt{32}$ cm
(B) $\sqrt{16}$ cm = 4 cm
(C) $\sqrt{48}$ cm
(D) $\sqrt{24}$ cm
The calculated length of the hypotenuse is $\sqrt{32}$ cm, which matches option (A).
The correct option is (A) $\sqrt{32}$ cm.
Question 2. The perimeter of an equilateral triangle is 60 m. The area is
(A) 10$\sqrt{3}$ m2
(B) 15$\sqrt{3}$ m2
(C) 20$\sqrt{3}$ m2
(D) 100$\sqrt{3}$ m2
Answer:
Given:
Perimeter of an equilateral triangle = $60$ m.
To Find:
The area of the equilateral triangle.
Solution:
Let the side length of the equilateral triangle be $a$ metres.
The perimeter of an equilateral triangle is given by $3 \times \text{side length}$.
So, Perimeter $= 3a$.
We are given that the perimeter is $60$ m.
Therefore, $3a = 60$.
Dividing both sides by $3$, we get:
$a = \frac{60}{3}$
$a = 20$ m
The side length of the equilateral triangle is $20$ m.
The area of an equilateral triangle with side length $a$ is given by the formula:
Area $= \frac{\sqrt{3}}{4} a^2$
Substitute the value of $a = 20$ m into the formula:
Area $= \frac{\sqrt{3}}{4} (20)^2$
Area $= \frac{\sqrt{3}}{4} (400)$
Area $= \sqrt{3} \times \frac{400}{4}$
Area $= \sqrt{3} \times 100$
Area $= 100\sqrt{3}$ m$^2$
Comparing this result with the given options, we find that it matches option (D).
Thus, the area of the equilateral triangle is $100\sqrt{3}$ m$^2$.
The correct option is (D) $100\sqrt{3}$ m2.
Question 3. The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is
(A) 1322 cm2
(B) 1311 cm2
(C) 1344 cm2
(D) 1392 cm2
Answer:
Given:
The lengths of the sides of the triangle are $a = 56$ cm, $b = 60$ cm, and $c = 52$ cm.
To Find:
The area of the triangle.
Solution:
Since the triangle has unequal sides, we can use Heron's formula to find its area.
First, calculate the semi-perimeter ($s$) of the triangle, which is half the perimeter:
$s = \frac{a+b+c}{2}$
$s = \frac{56 + 60 + 52}{2}$
$s = \frac{168}{2}$
$s = 84$ cm
Now, apply Heron's formula for the area of a triangle:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values of $s, a, b,$ and $c$:
Area $= \sqrt{84(84-56)(84-60)(84-52)}$
Area $= \sqrt{84 \times 28 \times 24 \times 32}$
Now, let's find the prime factorization of each number inside the square root:
$84 = 2^2 \times 3 \times 7$
$28 = 2^2 \times 7$
$24 = 2^3 \times 3$
$32 = 2^5$
Substitute these factorizations into the area formula:
Area $= \sqrt{(2^2 \times 3 \times 7) \times (2^2 \times 7) \times (2^3 \times 3) \times (2^5)}$
Combine the powers of the prime factors:
Area $= \sqrt{2^{2+2+3+5} \times 3^{1+1} \times 7^{1+1}}$
Area $= \sqrt{2^{12} \times 3^2 \times 7^2}$
To find the square root, divide the exponents by 2:
Area $= 2^{12/2} \times 3^{2/2} \times 7^{2/2}$
Area $= 2^6 \times 3^1 \times 7^1$
Area $= 64 \times 3 \times 7$
Area $= 64 \times 21$
Area $= 1344$ cm$^2$
Comparing this result with the given options, we find that it matches option (C).
The correct option is (C) 1344 cm2.
Question 4. The area of an equilateral triangle with side 2$\sqrt{3}$ cm is
(A) 5.196 cm2
(B) 0.866 cm2
(C) 3.496 cm2
(D) 1.732 cm2
Answer:
Given:
Side of the equilateral triangle ($a$) $= 2\sqrt{3}$ cm.
To Find:
The area of the equilateral triangle.
Solution:
The formula for the area of an equilateral triangle with side length $a$ is:
Area $= \frac{\sqrt{3}}{4} a^2$
Substitute the given side length $a = 2\sqrt{3}$ cm into the formula:
Area $= \frac{\sqrt{3}}{4} (2\sqrt{3})^2$
First, calculate $(2\sqrt{3})^2$:
$(2\sqrt{3})^2 = (2)^2 \times (\sqrt{3})^2 = 4 \times 3 = 12$
Now, substitute this value back into the area formula:
Area $= \frac{\sqrt{3}}{4} \times 12$
Area $= \sqrt{3} \times \frac{12}{4}$
Area $= \sqrt{3} \times 3$
Area $= 3\sqrt{3}$ cm$^2$
To compare with the options, we can use the approximate value of $\sqrt{3} \approx 1.732$:
Area $\approx 3 \times 1.732$
Area $\approx 5.196$ cm$^2$
Comparing this result with the given options, we find that it matches option (A).
The correct option is (A) 5.196 cm2.
Question 5. The length of each side of an equilateral triangle having an area of 9$\sqrt{3}$ cm2 is
(A) 8 cm
(B) 36 cm
(C) 4 cm
(D) 6 cm
Answer:
Given:
Area of the equilateral triangle $= 9\sqrt{3}$ cm$^2$.
To Find:
The length of each side of the equilateral triangle.
Solution:
Let the side length of the equilateral triangle be $a$ cm.
The formula for the area of an equilateral triangle with side length $a$ is given by:
Area $= \frac{\sqrt{3}}{4} a^2$
We are given that the area is $9\sqrt{3}$ cm$^2$. Substitute this value into the formula:
$9\sqrt{3} = \frac{\sqrt{3}}{4} a^2$
To solve for $a^2$, multiply both sides of the equation by $\frac{4}{\sqrt{3}}$:
$9\sqrt{3} \times \frac{4}{\sqrt{3}} = a^2$
Cancel out the $\sqrt{3}$ terms:
$9 \times 4 = a^2$
$36 = a^2$
To find the value of $a$, take the square root of both sides. Since the side length must be positive, we take the positive square root:
$a = \sqrt{36}$
$a = 6$ cm
The length of each side of the equilateral triangle is $6$ cm.
Comparing this result with the given options, we find that it matches option (D).
The correct option is (D) 6 cm.
Question 6. If the area of an equilateral triangle is 16$\sqrt{3}$ cm2 , then the perimeter of the triangle is
(A) 48 cm
(B) 24 cm
(C) 12 cm
(D) 36 cm
Answer:
Given:
Area of the equilateral triangle $= 16\sqrt{3}$ cm$^2$.
To Find:
The perimeter of the equilateral triangle.
Solution:
Let the side length of the equilateral triangle be $a$ cm.
The formula for the area of an equilateral triangle with side length $a$ is given by:
Area $= \frac{\sqrt{3}}{4} a^2$
We are given that the area is $16\sqrt{3}$ cm$^2$. Substitute this value into the formula:
$16\sqrt{3} = \frac{\sqrt{3}}{4} a^2$
To solve for $a^2$, multiply both sides of the equation by $\frac{4}{\sqrt{3}}$:
$16\sqrt{3} \times \frac{4}{\sqrt{3}} = a^2$
Cancel out the $\sqrt{3}$ terms:
$16 \times 4 = a^2$
$64 = a^2$
To find the value of $a$, take the square root of both sides. Since the side length must be positive, we take the positive square root:
$a = \sqrt{64}$
$a = 8$ cm
The length of each side of the equilateral triangle is $8$ cm.
The perimeter of an equilateral triangle is given by $3 \times \text{side length}$.
Perimeter $= 3a$
Substitute the value of $a = 8$ cm:
Perimeter $= 3 \times 8$
Perimeter $= 24$ cm
Comparing this result with the given options, we find that it matches option (B).
The correct option is (B) 24 cm.
Question 7. The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude
(A) 16$\sqrt{5}$ cm
(B) 10$\sqrt{5}$ cm
(C) 24$\sqrt{5}$ cm
(D) 28 cm
Answer:
Given:
The lengths of the sides of the triangle are $a = 35$ cm, $b = 54$ cm, and $c = 61$ cm.
To Find:
The length of the longest altitude of the triangle.
Solution:
The longest altitude of a triangle is the altitude drawn to its shortest side.
The side lengths are 35 cm, 54 cm, and 61 cm.
The shortest side is 35 cm. Let this side be the base, $a = 35$ cm.
Let the longest altitude corresponding to this base be $h_a$.
The area of the triangle can be calculated using Heron's formula.
First, calculate the semi-perimeter ($s$):
$s = \frac{a+b+c}{2}$
$s = \frac{35+54+61}{2}$
$s = \frac{150}{2}$
$s = 75$ cm
Now, calculate the area using Heron's formula:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s-a = 75 - 35 = 40$
$s-b = 75 - 54 = 21$
$s-c = 75 - 61 = 14$
Substitute these values into Heron's formula:
Area $= \sqrt{75 \times 40 \times 21 \times 14}$
Factorize the numbers inside the square root:
$75 = 3 \times 5^2$
$40 = 2^3 \times 5$
$21 = 3 \times 7$
$14 = 2 \times 7$
Area $= \sqrt{(3 \times 5^2) \times (2^3 \times 5) \times (3 \times 7) \times (2 \times 7)}$
Combine the prime factors:
Area $= \sqrt{2^{3+1} \times 3^{1+1} \times 5^{2+1} \times 7^{1+1}}$
Area $= \sqrt{2^4 \times 3^2 \times 5^3 \times 7^2}$
Area $= \sqrt{2^4 \times 3^2 \times 5^2 \times 5 \times 7^2}$
Take the square root of the terms with even exponents:
Area $= 2^{4/2} \times 3^{2/2} \times 5^{2/2} \times 7^{2/2} \times \sqrt{5}$
Area $= 2^2 \times 3^1 \times 5^1 \times 7^1 \times \sqrt{5}$
Area $= 4 \times 3 \times 5 \times 7 \times \sqrt{5}$
Area $= 12 \times 35 \times \sqrt{5}$
Area $= 420\sqrt{5}$ cm$^2$
Now, the area of a triangle is also given by the formula:
Area $= \frac{1}{2} \times \text{base} \times \text{altitude}
Using the shortest side as the base ($a=35$ cm) and the longest altitude as $h_a$:
$420\sqrt{5} = \frac{1}{2} \times 35 \times h_a$
Multiply both sides by 2:
$2 \times 420\sqrt{5} = 35 \times h_a$
$840\sqrt{5} = 35 \times h_a$
Divide by 35 to find $h_a$:
$h_a = \frac{840\sqrt{5}}{35}$
Simplify the fraction $\frac{840}{35}$:
$\frac{840}{35} = \frac{168 \times 5}{7 \times 5} = \frac{168}{7} = 24$
So, $h_a = 24\sqrt{5}$ cm.
The length of the longest altitude is $24\sqrt{5}$ cm.
Comparing this result with the given options, we find that it matches option (C).
The correct option is (C) 24$\sqrt{5}$ cm.
Question 8. The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is
(A) $\sqrt{15}$ cm2
(B) $\sqrt{\frac{15}{2}}$ cm2
(C) 2$\sqrt{15}$ cm2
(D) 4$\sqrt{15}$ cm2
Answer:
Given:
An isosceles triangle with base $b = 2$ cm and equal sides $a = 4$ cm.
To Find:
The area of the triangle.
Solution:
Let the isosceles triangle be ABC, where AC = BC = 4 cm and AB = 2 cm. Draw an altitude CD from vertex C to the base AB. In an isosceles triangle, the altitude from the vertex between the equal sides bisects the base.
So, AD = DB = $\frac{1}{2} \times \text{AB} = \frac{1}{2} \times 2 = 1$ cm.
Now consider the right-angled triangle ADC. By the Pythagorean theorem, we have:
AC$^2$ = AD$^2$ + CD$^2$
Substitute the known values:
$4^2 = 1^2 + \text{CD}^2$
$16 = 1 + \text{CD}^2$
Subtract 1 from both sides:
$\text{CD}^2 = 16 - 1$
$\text{CD}^2 = 15$
Taking the square root of both sides (and considering only the positive value for length):
CD $= \sqrt{15}$ cm.
The altitude (height) of the triangle is $h = \sqrt{15}$ cm.
The area of a triangle is given by the formula:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Using the base AB = 2 cm and the height CD = $\sqrt{15}$ cm:
Area $= \frac{1}{2} \times 2 \times \sqrt{15}$
Area $= 1 \times \sqrt{15}$
Area $= \sqrt{15}$ cm$^2$
Comparing this result with the given options, we find that it matches option (A).
The correct option is (A) $\sqrt{15}$ cm2.
Question 9. The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is
(A) Rs 2.00
(B) Rs 2.16
(C) Rs 2.48
(D) Rs 3.00
Answer:
Given:
The sides of the triangular board are $a = 6$ cm, $b = 8$ cm, and $c = 10$ cm.
Cost of painting = 9 paise per cm$^2$.
To Find:
The total cost of painting the triangular board.
Solution:
First, we need to find the area of the triangular board.
Let the side lengths be $a=6$ cm, $b=8$ cm, and $c=10$ cm.
We can check if this is a right-angled triangle using the Pythagorean theorem ($a^2 + b^2 = c^2$):
$6^2 + 8^2 = 36 + 64 = 100$
$10^2 = 100$
Since $6^2 + 8^2 = 10^2$, the triangle is a right-angled triangle with sides 6 cm and 8 cm as the base and height, and 10 cm as the hypotenuse.
The area of a right-angled triangle is given by:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Area $= \frac{1}{2} \times 6 \text{ cm} \times 8 \text{ cm}$
Area $= \frac{1}{2} \times 48 \text{ cm}^2$
Area $= 24$ cm$^2$
Now, we need to calculate the cost of painting the board.
The cost is 9 paise per cm$^2$.
First, convert the cost per cm$^2$ from paise to rupees. Since 1 Rupee = 100 paise:
9 paise $= \frac{9}{100}$ Rupees $= 0.09$ Rupees
Total cost $= \text{Area} \times \text{Cost per cm}^2$ (in Rupees)
Total cost $= 24 \text{ cm}^2 \times 0.09 \text{ ₹/cm}^2$
Total cost $= 24 \times 0.09$ Rupees
Total cost $= 2.16$ Rupees
Alternate Solution (using Heron's Formula):
The sides are $a=6$ cm, $b=8$ cm, $c=10$ cm.
Calculate the semi-perimeter ($s$):
$s = \frac{a+b+c}{2} = \frac{6+8+10}{2} = \frac{24}{2} = 12$ cm
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Area $= \sqrt{12(12-6)(12-8)(12-10)}$
Area $= \sqrt{12 \times 6 \times 4 \times 2}$
Area $= \sqrt{576}$
Area $= 24$ cm$^2$
The total cost is $24 \text{ cm}^2 \times 9 \text{ paise/cm}^2 = 216$ paise.
Convert 216 paise to Rupees: $\frac{216}{100}$ ₹ $= 2.16$ ₹.
Comparing the result with the given options, we find that it matches option (B).
The correct option is (B) ₹ 2.16.
Sample Question 1 (Before Exercise 12.2)
Write True or False and justify your answer:
Sample Question 1: If a, b, c are the lengths of three sides of a triangle, then area of a triangle = $\sqrt{s(s-a)(s-b)(s-c)}$ where s = perimeter of triangle.
Answer:
Answer:
False.
Justification:
The formula for the area of a triangle with side lengths a, b, and c is indeed given by Heron's formula: Area $= \sqrt{s(s-a)(s-b)(s-c)}$.
However, the variable $s$ in Heron's formula represents the semi-perimeter of the triangle, not the perimeter.
The semi-perimeter $s$ is defined as half of the perimeter:
$s = \frac{a+b+c}{2}$
The statement incorrectly defines $s$ as the perimeter of the triangle.
Therefore, the given statement is false because of the incorrect definition of $s$.
Exercise 12.2
Write True or False and justify your answer:
Question 1. The area of a triangle with base 4 cm and height 6 cm is 24 cm2 .
Answer:
Answer:
False.
Justification:
The formula for the area of a triangle is given by:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Given base $= 4$ cm and height $= 6$ cm.
Substituting these values into the formula:
Area $= \frac{1}{2} \times 4 \text{ cm} \times 6 \text{ cm}$
Area $= \frac{1}{2} \times 24 \text{ cm}^2$
Area $= 12$ cm$^2$
The calculated area of the triangle is 12 cm$^2$, which is not equal to 24 cm$^2$.
Therefore, the statement is false.
Question 2. The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
Answer:
Answer:
True.
Justification:
The triangle ABC is given with AB = AC = 4 cm and $\angle A = 90^\circ$.
Since $\angle A = 90^\circ$, the triangle is a right-angled triangle at vertex A.
In a right-angled triangle, the two sides forming the right angle can be considered as the base and the height.
Here, AB and AC are the sides forming the right angle at A. We can take AB as the base and AC as the height (or vice versa).
The formula for the area of a right-angled triangle is:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Substitute the given values: base $= \text{AB} = 4$ cm and height $= \text{AC} = 4$ cm.
Area $= \frac{1}{2} \times 4 \text{ cm} \times 4 \text{ cm}$
Area $= \frac{1}{2} \times 16 \text{ cm}^2$
Area $= 8$ cm$^2$
The calculated area of the triangle is 8 cm$^2$, which matches the area given in the statement.
Therefore, the statement is true.
Question 3. The area of the isosceles triangle is $\frac{5}{4}\sqrt{11}$ cm2 , if the perimeter is 11 cm and the base is 5 cm.
Answer:
Answer:
True.
Justification:
Let the isosceles triangle have equal sides of length $a$ and base of length $b$.
Given: Base $b = 5$ cm.
Given: Perimeter = 11 cm.
The perimeter of an isosceles triangle is $a + a + b = 2a + b$.
So, $2a + 5 = 11$.
$2a = 11 - 5$
$2a = 6$
$a = 3$ cm.
The side lengths of the triangle are 3 cm, 3 cm, and 5 cm.
To find the area, we can use Heron's formula. First, calculate the semi-perimeter ($s$).
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{11}{2}$ cm.
Now, calculate the terms for Heron's formula:
$s-a = \frac{11}{2} - 3 = \frac{11 - 6}{2} = \frac{5}{2}$
$s-b = \frac{11}{2} - 3 = \frac{11 - 6}{2} = \frac{5}{2}$
$s-c = \frac{11}{2} - 5 = \frac{11 - 10}{2} = \frac{1}{2}$
Heron's formula for the area of a triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area $= \sqrt{\frac{11}{2} \times \frac{5}{2} \times \frac{5}{2} \times \frac{1}{2}}$
Area $= \sqrt{\frac{11 \times 5 \times 5 \times 1}{2 \times 2 \times 2 \times 2}}$
Area $= \sqrt{\frac{25 \times 11}{16}}$
Area $= \frac{\sqrt{25} \times \sqrt{11}}{\sqrt{16}}$
Area $= \frac{5 \times \sqrt{11}}{4}$
Area $= \frac{5\sqrt{11}}{4}$ cm$^2$.
The calculated area matches the area given in the statement.
Therefore, the statement is true.
Question 4. The area of the equilateral triangle is 20$\sqrt{3}$ cm2 whose each side is 8 cm.
Answer:
Answer:
False.
Justification:
Let the side length of the equilateral triangle be $a$.
Given: Side length $a = 8$ cm.
The formula for the area of an equilateral triangle with side length $a$ is given by:
Area $= \frac{\sqrt{3}}{4} a^2$
Substitute the given side length $a = 8$ cm into the formula:
Area $= \frac{\sqrt{3}}{4} (8)^2$
Area $= \frac{\sqrt{3}}{4} \times 64$
Area $= \sqrt{3} \times \frac{64}{4}$
Area $= \sqrt{3} \times 16$
Area $= 16\sqrt{3}$ cm$^2$
The calculated area of the equilateral triangle is $16\sqrt{3}$ cm$^2$.
The statement claims the area is $20\sqrt{3}$ cm$^2$.
Since $16\sqrt{3} \neq 20\sqrt{3}$, the statement is false.
Question 5. If the side of a rhombus is 10 cm and one diagonal is 16 cm, the area of the rhombus is 96 cm2 .
Answer:
Answer:
True.
Justification:
Let the side of the rhombus be $a = 10$ cm.
Let one diagonal be $d_1 = 16$ cm.
The diagonals of a rhombus bisect each other at right angles.
Let the half-lengths of the diagonals be $\frac{d_1}{2}$ and $\frac{d_2}{2}$, where $d_2$ is the length of the other diagonal.
The half-diagonals and the side of the rhombus form a right-angled triangle, with the side as the hypotenuse.
So, by the Pythagorean theorem:
$(\frac{d_1}{2})^2 + (\frac{d_2}{2})^2 = a^2$
Substitute the given values:
$(\frac{16}{2})^2 + (\frac{d_2}{2})^2 = 10^2$
$8^2 + (\frac{d_2}{2})^2 = 100$
$64 + (\frac{d_2}{2})^2 = 100$
$(\frac{d_2}{2})^2 = 100 - 64 = 36$
Taking the square root of both sides (since length is positive):
$\frac{d_2}{2} = \sqrt{36} = 6$
So, the length of the other diagonal is $d_2 = 2 \times 6 = 12$ cm.
The area of a rhombus is given by the formula:
Area $= \frac{1}{2} \times d_1 \times d_2$
Substitute the values of the diagonals:
Area $= \frac{1}{2} \times 16 \text{ cm} \times 12 \text{ cm}$
Area $= \frac{1}{2} \times 192 \text{ cm}^2$
Area $= 96$ cm$^2$
The calculated area is 96 cm$^2$, which matches the area given in the statement.
Therefore, the statement is true.
Question 6. The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2 .
Answer:
Answer:
False.
Justification:
The area of a parallelogram is given by the formula:
Area $= \text{base} \times \text{altitude}$
Given: Base $= 10$ cm.
Given: Corresponding altitude $= 3.5$ cm.
Substitute the given values into the formula:
Area $= 10 \text{ cm} \times 3.5 \text{ cm}$
Area $= 35$ cm$^2$
The calculated area of the parallelogram is 35 cm$^2$.
The statement claims the area is 30 cm$^2$.
Since $35 \text{ cm}^2 \neq 30 \text{ cm}^2$, the statement is false.
Question 7. The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
Answer:
Answer:
False.
Justification:
A regular hexagon is a polygon with six equal sides and six equal interior angles.
A regular hexagon can be divided into six congruent equilateral triangles by drawing lines from the center to each vertex.
If the side length of the regular hexagon is $a$, then the side length of each of these six equilateral triangles is also $a$.
The formula for the area of an equilateral triangle with side length $a$ is:
Area of one equilateral triangle $= \frac{\sqrt{3}}{4} a^2$
The area of the regular hexagon is the sum of the areas of these six equilateral triangles:
Area of regular hexagon $= 6 \times (\text{Area of one equilateral triangle})$
Area of regular hexagon $= 6 \times \frac{\sqrt{3}}{4} a^2$
Area of regular hexagon $= \frac{6\sqrt{3}}{4} a^2 = \frac{3\sqrt{3}}{2} a^2$
The statement claims that the area of the regular hexagon is the sum of the areas of five equilateral triangles with side $a$, which would be $5 \times \frac{\sqrt{3}}{4} a^2 = \frac{5\sqrt{3}}{4} a^2$.
Since $\frac{6\sqrt{3}}{4} a^2 \neq \frac{5\sqrt{3}}{4} a^2$, the statement is incorrect.
A regular hexagon of side $a$ is composed of six equilateral triangles of side $a$, not five.
Therefore, the statement is false.
Question 8. The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
Answer:
Answer:
True.
Justification:
Given the side lengths of the triangular ground: $a = 51$ m, $b = 37$ m, and $c = 20$ m.
To find the area of the triangle, we use Heron's formula.
First, calculate the semi-perimeter ($s$).
$s = \frac{a+b+c}{2}$
$s = \frac{51 + 37 + 20}{2}$
$s = \frac{108}{2}$
$s = 54$ m
Now, calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$.
$s-a = 54 - 51 = 3$
$s-b = 54 - 37 = 17$
$s-c = 54 - 20 = 34$
Heron's formula for the area of a triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area $= \sqrt{54 \times 3 \times 17 \times 34}$
Factorize the numbers inside the square root:
$54 = 2 \times 3 \times 3 \times 3 = 2 \times 3^3$
$3 = 3^1$
$17 = 17^1$
$34 = 2 \times 17 = 2^1 \times 17^1$
Area $= \sqrt{(2^1 \times 3^3) \times 3^1 \times 17^1 \times (2^1 \times 17^1)}$
Combine the powers of the prime factors:
Area $= \sqrt{2^{1+1} \times 3^{3+1} \times 17^{1+1}}$
Area $= \sqrt{2^2 \times 3^4 \times 17^2}$
Take the square root by dividing the exponents by 2:
Area $= 2^{2/2} \times 3^{4/2} \times 17^{2/2}$
Area $= 2^1 \times 3^2 \times 17^1$
Area $= 2 \times 9 \times 17$
Area $= 18 \times 17$
Area $= 306$ m$^2$
The cost of levelling is ₹ 3 per m$^2$.
Total cost $= \text{Area} \times \text{Cost per unit area}$
Total cost $= 306 \text{ m}^2 \times \textsf{₹} 3/\text{m}^2$
Total cost $= 306 \times 3$ ₹
Total cost $= 918$ ₹
The calculated cost of levelling is ₹ 918, which matches the cost given in the statement.
Therefore, the statement is true.
Question 9. In a triangle, the sides are given as 11cm, 12cm and 13cm. The length of the altitude is 10.25 cm corresponding to the side having length 12cm.
Answer:
Answer:
False.
Justification:
Let the sides of the triangle be $a = 11$ cm, $b = 12$ cm, and $c = 13$ cm.
First, we calculate the area of the triangle using Heron's formula.
The semi-perimeter $s$ is given by:
$s = \frac{a+b+c}{2}$
$s = \frac{11 + 12 + 13}{2}$
$s = \frac{36}{2}$
$s = 18$ cm
The area of the triangle is given by:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s-a = 18 - 11 = 7$
$s-b = 18 - 12 = 6$
$s-c = 18 - 13 = 5$
Substitute these values into Heron's formula:
Area $= \sqrt{18 \times 7 \times 6 \times 5}$
Area $= \sqrt{(2 \times 3^2) \times 7 \times (2 \times 3) \times 5}$
Area $= \sqrt{2^{1+1} \times 3^{2+1} \times 5 \times 7}$
Area $= \sqrt{2^2 \times 3^3 \times 5 \times 7}$
Area $= \sqrt{2^2 \times 3^2 \times 3 \times 5 \times 7}$
Area $= 2 \times 3 \times \sqrt{3 \times 5 \times 7}$
Area $= 6\sqrt{105}$ cm$^2$
Now, we can find the altitude corresponding to the side with length 12 cm (let's take base $= 12$ cm and altitude $= h$). The area of a triangle is also given by:
Area $= \frac{1}{2} \times \text{base} \times \text{altitude}$
Substitute the area and the base:
$6\sqrt{105} = \frac{1}{2} \times 12 \times h$
$6\sqrt{105} = 6h$
Divide both sides by 6:
$h = \sqrt{105}$ cm
The actual length of the altitude corresponding to the side of length 12 cm is $\sqrt{105}$ cm.
The value of $\sqrt{105}$ is approximately:
$\sqrt{105} \approx 10.24695...$
The statement claims the altitude is 10.25 cm. Since $\sqrt{105} \neq 10.25$, the statement is false.
Sample Question 1 & 2 (Before Exercise 12.3)
Sample Question 1: The sides of a triangular field are 41 m, 40 m and 9 m. Find the number of rose beds that can be prepared in the field, if each rose bed, on an average needs 900 cm2 space.
Answer:
Given:
Sides of the triangular field are $a = 41$ m, $b = 40$ m, and $c = 9$ m.
Space needed per rose bed $= 900$ cm$^2$.
To Find:
The number of rose beds that can be prepared in the field.
Solution:
First, calculate the area of the triangular field.
Let the side lengths be $a = 41$ m, $b = 40$ m, and $c = 9$ m.
We can check if this is a right-angled triangle by checking if the square of the longest side is equal to the sum of the squares of the other two sides.
$9^2 + 40^2 = 81 + 1600 = 1681$
$41^2 = 1681$
Since $9^2 + 40^2 = 41^2$, the triangle is a right-angled triangle with sides 9 m and 40 m as the base and height, and 41 m as the hypotenuse.
The area of a right-angled triangle is given by:
Area of triangle $= \frac{1}{2} \times \text{base} \times \text{height}
Area of triangle $= \frac{1}{2} \times 9 \text{ m} \times 40 \text{ m}$
Area of triangle $= \frac{1}{2} \times 360 \text{ m}^2$
Area of triangle $= 180$ m$^2$
Alternatively, using Heron's formula:
Semi-perimeter $s = \frac{41 + 40 + 9}{2} = \frac{90}{2} = 45$ m
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Area $= \sqrt{45(45-41)(45-40)(45-9)}$
Area $= \sqrt{45 \times 4 \times 5 \times 36}$
Area $= \sqrt{(9 \times 5) \times 4 \times 5 \times 36}$
Area $= \sqrt{9 \times 4 \times 36 \times 5 \times 5}$
Area $= \sqrt{9} \times \sqrt{4} \times \sqrt{36} \times \sqrt{5^2}$
Area $= 3 \times 2 \times 6 \times 5$
Area $= 180$ m$^2$
Now, convert the area of the field from m$^2$ to cm$^2$, since the space needed per rose bed is given in cm$^2$.
$1 \text{ m} = 100 \text{ cm}$
$1 \text{ m}^2 = (100 \text{ cm})^2 = 10000 \text{ cm}^2$
Area of triangular field in cm$^2 = 180 \text{ m}^2 \times 10000 \text{ cm}^2/\text{m}^2$
Area of triangular field $= 1800000$ cm$^2$
The space needed per rose bed is 900 cm$^2$.
Number of rose beds $= \frac{\text{Total area of the field}}{\text{Space needed per rose bed}}$
Number of rose beds $= \frac{1800000 \text{ cm}^2}{900 \text{ cm}^2/\text{rose bed}}$
Number of rose beds $= \frac{1800000}{900}$
Number of rose beds $= \frac{18000}{9}$
Number of rose beds $= 2000$
Therefore, 2000 rose beds can be prepared in the field.
Sample Question 2: Calculate the area of the shaded region in Fig. 12.1.
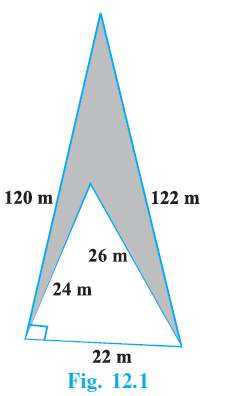
Answer:
Given:
Rectangle ABCD with length AB = 18 cm and breadth AD = 10 cm.
Point E is on AB such that AE = 10 cm.
Point F is on AD such that AF = 6 cm.
The shaded region is the quadrilateral EFCD.
To Find:
The area of the shaded region.
Solution:
The shaded region (quadrilateral EFCD) is the area of the rectangle ABCD minus the areas of the two unshaded triangles, AFE and EBC.
First, calculate the area of the rectangle ABCD.
Area(Rectangle ABCD) $=$ length $\times$ breadth
Area(Rectangle ABCD) $=$ AB $\times$ AD
Area(Rectangle ABCD) $=$ $18 \text{ cm} \times 10 \text{ cm}$
Area(Rectangle ABCD) $=$ $180$ cm$^2$
Next, calculate the area of the unshaded triangle AFE.
Triangle AFE is a right-angled triangle at A (since ABCD is a rectangle).
Base AE $= 10$ cm
Height AF $= 6$ cm
Area(Triangle AFE) $=$ $\frac{1}{2} \times \text{base} \times \text{height}
Area(Triangle AFE) $=$ $\frac{1}{2} \times \text{AE} \times \text{AF}
Area(Triangle AFE) $=$ $\frac{1}{2} \times 10 \text{ cm} \times 6 \text{ cm}
Area(Triangle AFE) $=$ $\frac{1}{2} \times 60 \text{ cm}^2$
Area(Triangle AFE) $=$ $30$ cm$^2$
Now, calculate the area of the unshaded triangle EBC.
To find the length of EB, we subtract AE from AB.
EB $=$ AB $-$ AE
EB $=$ $18 \text{ cm} - 10 \text{ cm}$
EB $=$ $8$ cm
Triangle EBC is a right-angled triangle at B (since ABCD is a rectangle).
Base EB $= 8$ cm
Height BC $= 10$ cm
Area(Triangle EBC) $=$ $\frac{1}{2} \times \text{base} \times \text{height}
Area(Triangle EBC) $=$ $\frac{1}{2} \times \text{EB} \times \text{BC}
Area(Triangle EBC) $=$ $\frac{1}{2} \times 8 \text{ cm} \times 10 \text{ cm}
Area(Triangle EBC) $=$ $\frac{1}{2} \times 80 \text{ cm}^2$
Area(Triangle EBC) $=$ $40$ cm$^2$
The area of the shaded region is the area of the rectangle minus the sum of the areas of the two unshaded triangles.
Area(Shaded region) $=$ Area(Rectangle ABCD) $-$ (Area(Triangle AFE) $+$ Area(Triangle EBC))
Area(Shaded region) $=$ $180 \text{ cm}^2 - (30 \text{ cm}^2 + 40 \text{ cm}^2)$
Area(Shaded region) $=$ $180 \text{ cm}^2 - 70 \text{ cm}^2$
Area(Shaded region) $=$ $110$ cm$^2$
The area of the shaded region is 110 cm$^2$.
Exercise 12.3
Question 1. Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2 .
Answer:
Given:
The lengths of the sides of the triangular field are $a = 50$ m, $b = 65$ m, and $c = 65$ m.
The rate of laying grass is $\textsf{₹} 7$ per m$^2$.
To Find:
The cost of laying grass in the triangular field.
Solution:
First, we need to find the area of the triangular field. Since the sides are given, we can use Heron's formula.
Calculate the semi-perimeter ($s$) of the triangle:
$s = \frac{a+b+c}{2}$
$s = \frac{50 + 65 + 65}{2}$
$s = \frac{180}{2}$
$s = 90$ m
Now, calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s-a = 90 - 50 = 40$
$s-b = 90 - 65 = 25$
$s-c = 90 - 65 = 25$
Heron's formula for the area of a triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area $= \sqrt{90 \times 40 \times 25 \times 25}$
Area $= \sqrt{(9 \times 10) \times (4 \times 10) \times 25 \times 25}$
Area $= \sqrt{9 \times 4 \times 10 \times 10 \times 25 \times 25}$
Area $= \sqrt{9 \times 4 \times 100 \times 625}$
Area $= \sqrt{9} \times \sqrt{4} \times \sqrt{100} \times \sqrt{625}$
Area $= 3 \times 2 \times 10 \times 25$
Area $= 6 \times 250$
Area $= 1500$ m$^2$
The area of the triangular field is 1500 m$^2$.
The cost of laying grass is $\textsf{₹} 7$ per m$^2$.
Total cost $=$ Area $\times$ Rate per m$^2$
Total cost $=$ $1500 \text{ m}^2 \times \textsf{₹} 7/\text{m}^2$
Total cost $=$ $1500 \times 7$ $\textsf{₹}$
Total cost $=$ $10500$ $\textsf{₹}$
The cost of laying grass in the field is $\textsf{₹} 10500$.
Question 2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs. 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
Answer:
Given:
The sides of the triangular wall are $a = 13$ m, $b = 14$ m, and $c = 15$ m.
Annual earning rate from advertisement $= \textsf{₹} 2000$ per m$^2$ per year.
Time period for which the wall was hired $= 6$ months.
To Find:
The total rent paid for hiring the wall for 6 months.
Solution:
First, we need to find the area of the triangular wall using Heron's formula.
Calculate the semi-perimeter ($s$) of the triangle:
$s = \frac{a+b+c}{2}$
$s = \frac{13 + 14 + 15}{2}$
$s = \frac{42}{2}$
$s = 21$ m
Now, calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s-a = 21 - 13 = 8$
$s-b = 21 - 14 = 7$
$s-c = 21 - 15 = 6$
Heron's formula for the area of a triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area $= \sqrt{21 \times 8 \times 7 \times 6}$
Factorize the numbers inside the square root:
$21 = 3 \times 7$
$8 = 2^3$
$7 = 7^1$
$6 = 2 \times 3 = 2^1 \times 3^1$
Area $= \sqrt{(3 \times 7) \times (2^3) \times 7 \times (2 \times 3)}$
Combine the powers of the prime factors:
Area $= \sqrt{2^{3+1} \times 3^{1+1} \times 7^{1+1}}$
Area $= \sqrt{2^4 \times 3^2 \times 7^2}$
Take the square root by dividing the exponents by 2:
Area $= 2^{4/2} \times 3^{2/2} \times 7^{2/2}$
Area $= 2^2 \times 3^1 \times 7^1$
Area $= 4 \times 3 \times 7$
Area $= 12 \times 7$
Area $= 84$ m$^2$
The area of the triangular wall is 84 m$^2$.
The advertisement earning rate is $\textsf{₹} 2000$ per m$^2$ per year.
The wall was hired for 6 months, which is $\frac{6}{12} = \frac{1}{2}$ a year.
The earning rate for 6 months will be half of the annual rate.
Earning rate for 6 months $= \frac{1}{2} \times \textsf{₹} 2000 \text{ per m}^2 \text{ per year}$
Earning rate for 6 months $= \textsf{₹} 1000$ per m$^2$ for 6 months.
The total rent paid is the area of the wall multiplied by the rate for 6 months.
Total Rent $=$ Area $\times$ Rate for 6 months
Total Rent $=$ $84 \text{ m}^2 \times \textsf{₹} 1000/\text{m}^2$
Total Rent $=$ $84 \times 1000$ $\textsf{₹}$
Total Rent $=$ $84000$ $\textsf{₹}$
The company paid a rent of $\textsf{₹} 84000$ for hiring the wall for 6 months.
Question 3. From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are 14 cm, 10 cm and 6 cm. Find the area of the triangle.
Answer:
Given:
An equilateral triangle. Perpendiculars from an interior point to the sides have lengths $p_1 = 14$ cm, $p_2 = 10$ cm, and $p_3 = 6$ cm.
To Find:
The area of the equilateral triangle.
Solution:
Let the side length of the equilateral triangle be $a$ cm.
Let the altitude (height) of the equilateral triangle be $h$ cm.
A property of equilateral triangles states that the sum of the lengths of the perpendiculars drawn from any interior point to the three sides is equal to the altitude of the triangle.
So, $h = p_1 + p_2 + p_3$
Substitute the given lengths of the perpendiculars:
$h = 14 + 10 + 6$
$h = 30$ cm
The relationship between the altitude ($h$) and the side length ($a$) of an equilateral triangle is given by:
$h = \frac{\sqrt{3}}{2} a$
Substitute the calculated altitude $h = 30$ cm:
$30 = \frac{\sqrt{3}}{2} a$
Solve for $a$:
$a = \frac{2 \times 30}{\sqrt{3}}$
$a = \frac{60}{\sqrt{3}}$
Rationalize the denominator:
$a = \frac{60}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{60\sqrt{3}}{3}$
$a = 20\sqrt{3}$ cm
The side length of the equilateral triangle is $20\sqrt{3}$ cm.
The area of an equilateral triangle with side length $a$ is given by the formula:
Area $= \frac{\sqrt{3}}{4} a^2$
Substitute the value of $a = 20\sqrt{3}$ cm:
Area $= \frac{\sqrt{3}}{4} (20\sqrt{3})^2$
Calculate $(20\sqrt{3})^2$:
$(20\sqrt{3})^2 = 20^2 \times (\sqrt{3})^2 = 400 \times 3 = 1200$
Substitute this value back into the area formula:
Area $= \frac{\sqrt{3}}{4} \times 1200$
Area $= \sqrt{3} \times \frac{1200}{4}$
Area $= \sqrt{3} \times 300$
Area $= 300\sqrt{3}$ cm$^2$
The area of the triangle is $300\sqrt{3}$ cm$^2$.
Question 4. The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
Answer:
Given:
Perimeter of an isosceles triangle $= 32$ cm.
Ratio of equal side to base $= 3:2$.
To Find:
The area of the triangle.
Solution:
Let the length of the equal sides be $3x$ cm and the length of the base be $2x$ cm, based on the given ratio of 3:2.
The perimeter of the isosceles triangle is the sum of the lengths of its sides:
Perimeter $=$ Equal side $+$ Equal side $+$ Base
Perimeter $=$ $3x + 3x + 2x$
Perimeter $=$ $8x$
We are given that the perimeter is 32 cm.
So, $8x = 32$.
Divide both sides by 8:
$x = \frac{32}{8}$
$x = 4$
Now, find the actual lengths of the sides:
Equal side $= 3x = 3 \times 4 = 12$ cm
Base $= 2x = 2 \times 4 = 8$ cm
The sides of the triangle are 12 cm, 12 cm, and 8 cm.
To find the area, we can use Heron's formula.
The semi-perimeter ($s$) is half the perimeter:
$s = \frac{32}{2} = 16$ cm
Calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$, where $a=12$, $b=12$, and $c=8$:
$s-a = 16 - 12 = 4$
$s-b = 16 - 12 = 4$
$s-c = 16 - 8 = 8$
Heron's formula for the area of a triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area $= \sqrt{16 \times 4 \times 4 \times 8}$
Area $= \sqrt{16 \times 16 \times 8}$
Area $= \sqrt{16^2 \times 8}$
Area $= 16 \sqrt{8}$
Simplify $\sqrt{8}$:
$\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}$
Substitute this back into the area calculation:
Area $= 16 \times 2\sqrt{2}$
Area $= 32\sqrt{2}$ cm$^2$
The area of the triangle is $32\sqrt{2}$ cm$^2$.
Alternate Solution (using altitude):
In an isosceles triangle, the altitude to the base bisects the base.
Base $= 8$ cm, so half of the base is 4 cm.
Equal side $= 12$ cm.
Let the altitude to the base be $h$. This forms a right-angled triangle with the equal side (hypotenuse), half of the base (one leg), and the altitude (the other leg).
By the Pythagorean theorem:
$(\text{Half base})^2 + h^2 = (\text{Equal side})^2$
$4^2 + h^2 = 12^2$
$16 + h^2 = 144$
$h^2 = 144 - 16$
$h^2 = 128$
$h = \sqrt{128}$
$h = \sqrt{64 \times 2} = \sqrt{64} \times \sqrt{2} = 8\sqrt{2}$ cm
Area of triangle $= \frac{1}{2} \times \text{base} \times \text{height}
Area $= \frac{1}{2} \times 8 \text{ cm} \times 8\sqrt{2} \text{ cm}
Area $= 4 \times 8\sqrt{2} \text{ cm}^2$
Area $= 32\sqrt{2}$ cm$^2$
Both methods yield the same area.
Question 5. Find the area of a parallelogram given in Fig. 12.2. Also find the length of the altitude from vertex A on the side DC.

Answer:
Given:
A parallelogram ABCD with side lengths AB = BC = CD = AD = 12 cm. (Note: Since all sides are equal, this is a rhombus).
Altitude from vertex B to the extension of side DC is BE = 5 cm.
To Find:
1. The area of parallelogram ABCD.
2. The length of the altitude from vertex A on the side DC.
Solution:
1. Area of the parallelogram:
The area of a parallelogram is given by the formula:
Area $=$ Base $\times$ Corresponding Altitude
From the figure, we can take the base as DC. The length of side DC is 12 cm.
The altitude corresponding to the base DC is BE, which is perpendicular to the extension of DC. The length of BE is 5 cm.
Area(Parallelogram ABCD) $=$ DC $\times$ BE
Area(Parallelogram ABCD) $=$ $12 \text{ cm} \times 5 \text{ cm}$
Area(Parallelogram ABCD) $=$ $60$ cm$^2$
The area of the parallelogram is 60 cm$^2$.
2. Length of the altitude from vertex A on the side DC:
Let $h$ be the length of the altitude from vertex A on the side DC.
The side DC is parallel to the side AB. The altitude from A to DC represents the perpendicular distance between the parallel lines AB and DC.
The area of the parallelogram can also be calculated using the base DC and the altitude $h$ from A to DC:
Area(Parallelogram ABCD) $=$ DC $\times h$
We know the Area is 60 cm$^2$ and DC is 12 cm.
$60 \text{ cm}^2 = 12 \text{ cm} \times h$
To find $h$, divide the area by the base:
$h = \frac{60 \text{ cm}^2}{12 \text{ cm}}$
$h = 5$ cm
The length of the altitude from vertex A on the side DC is 5 cm.
(Note: Since ABCD is a rhombus, the altitude corresponding to any side is the same, which is 5 cm in this case).
Question 6. A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
Answer:
Given:
A parallelogram with adjacent sides $a = 60$ m and $b = 40$ m.
One diagonal is $d = 80$ m.
To Find:
The area of the parallelogram.
Solution:
A parallelogram is divided into two congruent triangles by its diagonal.
Let the parallelogram be ABCD, with AB = CD = 60 m and BC = AD = 40 m.
Let the diagonal be AC = 80 m.
The diagonal AC divides the parallelogram into two triangles, $\triangle$ABC and $\triangle$ADC.
The sides of $\triangle$ABC are AB = 60 m, BC = 40 m, and AC = 80 m.
The sides of $\triangle$ADC are AD = 40 m, DC = 60 m, and AC = 80 m.
Since the corresponding sides are equal, $\triangle$ABC is congruent to $\triangle$ADC.
The area of the parallelogram is twice the area of either of these triangles.
Let's calculate the area of $\triangle$ABC using Heron's formula with sides 60 m, 40 m, and 80 m.
Calculate the semi-perimeter ($s$) of $\triangle$ABC:
$s = \frac{60 + 40 + 80}{2}$
$s = \frac{180}{2}$
$s = 90$ m
Now, calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$ for $\triangle$ABC, where $a=60$, $b=40$, and $c=80$:
$s-a = 90 - 60 = 30$
$s-b = 90 - 40 = 50$
$s-c = 90 - 80 = 10$
Heron's formula for the area of a triangle is:
Area(Triangle ABC) $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area(Triangle ABC) $= \sqrt{90 \times 30 \times 50 \times 10}$
Factorize the numbers inside the square root:
$90 = 9 \times 10 = 3^2 \times 10$
$30 = 3 \times 10$
$50 = 5 \times 10$
$10 = 10$
Area(Triangle ABC) $= \sqrt{(3^2 \times 10) \times (3 \times 10) \times (5 \times 10) \times 10}$
Combine the powers of the prime factors:
Area(Triangle ABC) $= \sqrt{3^{2+1} \times 5^1 \times 10^{1+1+1+1}}$
Area(Triangle ABC) $= \sqrt{3^3 \times 5^1 \times 10^4}$
Area(Triangle ABC) $= \sqrt{3^2 \times 3 \times 5 \times 10^4}$
Area(Triangle ABC) $= 3 \times 10^{4/2} \times \sqrt{3 \times 5}$
Area(Triangle ABC) $= 3 \times 10^2 \times \sqrt{15}$
Area(Triangle ABC) $= 300\sqrt{15}$ m$^2$
The area of the parallelogram is twice the area of $\triangle$ABC.
Area(Parallelogram ABCD) $= 2 \times$ Area(Triangle ABC)
Area(Parallelogram ABCD) $= 2 \times 300\sqrt{15}$ m$^2$
Area(Parallelogram ABCD) $= 600\sqrt{15}$ m$^2$
The area of the parallelogram is $600\sqrt{15}$ m$^2$.
Question 7. The perimeter of a triangular field is 420 m and its sides are in the ratio 6 : 7 : 8. Find the area of the triangular field.
Answer:
Given:
Perimeter of the triangular field $= 420$ m.
Ratio of the sides $= 6 : 7 : 8$.
To Find:
The area of the triangular field.
Solution:
Let the sides of the triangular field be $6x$, $7x$, and $8x$ metres, according to the given ratio.
The perimeter of the triangle is the sum of its sides:
Perimeter $= 6x + 7x + 8x = 21x$
We are given that the perimeter is 420 m.
So, we have the equation:
$21x = 420$
Solving for $x$:
$x = \frac{420}{21}$
$x = 20$
Now, find the actual lengths of the sides:
Side 1 ($a$) $= 6x = 6 \times 20 = 120$ m
Side 2 ($b$) $= 7x = 7 \times 20 = 140$ m
Side 3 ($c$) $= 8x = 8 \times 20 = 160$ m
The sides of the triangle are 120 m, 140 m, and 160 m.
To find the area of the triangle, we use Heron's formula.
First, calculate the semi-perimeter ($s$). The semi-perimeter is half of the perimeter.
$s = \frac{\text{Perimeter}}{2} = \frac{420}{2} = 210$ m
Now, calculate the differences between the semi-perimeter and each side:
$s-a = 210 - 120 = 90$
$s-b = 210 - 140 = 70$
$s-c = 210 - 160 = 50$
Heron's formula for the area of a triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values into the formula:
Area $= \sqrt{210 \times 90 \times 70 \times 50}$
Now, simplify the expression under the square root:
Area $= \sqrt{(21 \times 10) \times (9 \times 10) \times (7 \times 10) \times (5 \times 10)}$
Area $= \sqrt{21 \times 9 \times 7 \times 5 \times 10^4}
Area $= \sqrt{(3 \times 7) \times 3^2 \times 7 \times 5 \times (10^2)^2}
Area $= \sqrt{3^3 \times 5 \times 7^2 \times 10^4}$
Area $= \sqrt{3^2 \times 3 \times 5 \times 7^2 \times (10^2)^2}$
Area $= \sqrt{3^2} \times \sqrt{7^2} \times \sqrt{10^4} \times \sqrt{3 \times 5}
Area $= 3 \times 7 \times 10^2 \times \sqrt{15}
Area $= 21 \times 100 \times \sqrt{15}
Area $= 2100\sqrt{15}$ m$^2$
The area of the triangular field is $2100\sqrt{15}$ m$^2$.
Question 8. The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
Answer:
Given:
A quadrilateral ABCD with side lengths:
AB = 6 cm
BC = 8 cm
CD = 12 cm
DA = 14 cm
The angle between the first two sides (AB and BC) is a right angle, so $\angle \text{ABC} = 90^\circ$.
To Find:
The area of the quadrilateral ABCD.
Solution:
We can divide the quadrilateral ABCD into two triangles by drawing the diagonal AC.
The area of the quadrilateral will be the sum of the areas of $\triangle$ABC and $\triangle$ADC.
1. Calculate the area of $\triangle$ABC:
$\triangle$ABC is a right-angled triangle at B, with sides AB = 6 cm and BC = 8 cm.
The area of a right-angled triangle is given by:
Area($\triangle$ABC) $= \frac{1}{2} \times \text{base} \times \text{height}
Area($\triangle$ABC) $= \frac{1}{2} \times \text{AB} \times \text{BC}
Area($\triangle$ABC) $= \frac{1}{2} \times 6 \text{ cm} \times 8 \text{ cm}
Area($\triangle$ABC) $= \frac{1}{2} \times 48 \text{ cm}^2
Area($\triangle$ABC) $= 24$ cm$^2$
2. Calculate the length of the diagonal AC:
In the right-angled $\triangle$ABC, we can use the Pythagorean theorem to find the length of the hypotenuse AC.
AC$^2$ $=$ AB$^2$ $+$ BC$^2$
AC$^2$ $=$ $(6 \text{ cm})^2 + (8 \text{ cm})^2$
AC$^2$ $=$ $36 \text{ cm}^2 + 64 \text{ cm}^2$
AC$^2$ $=$ $100 \text{ cm}^2$
AC $=$ $\sqrt{100 \text{ cm}^2}$
AC $=$ $10$ cm
3. Calculate the area of $\triangle$ADC:
The sides of $\triangle$ADC are AD = 14 cm, CD = 12 cm, and AC = 10 cm.
We can use Heron's formula to find the area of $\triangle$ADC.
First, calculate the semi-perimeter ($s'$) of $\triangle$ADC:
$s' = \frac{\text{AD} + \text{CD} + \text{AC}}{2}$
$s' = \frac{14 + 12 + 10}{2}$
$s' = \frac{36}{2}$
$s' = 18$ cm
Now, calculate the terms $(s'-\text{AD})$, $(s'-\text{CD})$, and $(s'-\text{AC})$:
$s'-\text{AD} = 18 - 14 = 4$
$s'-\text{CD} = 18 - 12 = 6$
$s'-\text{AC} = 18 - 10 = 8$
Heron's formula for the area of $\triangle$ADC is:
Area($\triangle$ADC) $= \sqrt{s'(s'-\text{AD})(s'-\text{CD})(s'-\text{AC})}$
Substitute the calculated values:
Area($\triangle$ADC) $= \sqrt{18 \times 4 \times 6 \times 8}
Factorize the numbers inside the square root:
Area($\triangle$ADC) $= \sqrt{(2 \times 3^2) \times 2^2 \times (2 \times 3) \times 2^3}
Combine the powers of the prime factors:
Area($\triangle$ADC) $= \sqrt{2^{1+2+1+3} \times 3^{2+1}} = \sqrt{2^7 \times 3^3}
Area($\triangle$ADC) $= \sqrt{2^6 \times 2 \times 3^2 \times 3} = \sqrt{(2^3)^2 \times 3^2 \times 2 \times 3}
Area($\triangle$ADC) $= 2^3 \times 3 \times \sqrt{2 \times 3} = 8 \times 3 \times \sqrt{6}
Area($\triangle$ADC) $= 24\sqrt{6}$ cm$^2$
4. Calculate the area of the quadrilateral ABCD:
Area(ABCD) $=$ Area($\triangle$ABC) $+$ Area($\triangle$ADC)
Area(ABCD) $=$ $24 \text{ cm}^2 + 24\sqrt{6} \text{ cm}^2$
Area(ABCD) $=$ $(24 + 24\sqrt{6})$ cm$^2$
Area(ABCD) $=$ $24(1 + \sqrt{6})$ cm$^2$
The area of the quadrilateral ABCD is $24(1 + \sqrt{6})$ cm$^2$.
Question 9. A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2 . Find the cost of painting.
Answer:
Given:
Perimeter of the rhombus $= 40$ cm.
Length of one diagonal ($d_1$) $= 12$ cm.
Rate of painting $= \textsf{₹} 5$ per m$^2$ on both sides.
To Find:
The total cost of painting the rhombus shaped sheet on both sides.
Solution:
First, find the side length of the rhombus.
The perimeter of a rhombus is $4 \times \text{side}$.
Let the side length be $a$. So, $4a = 40$ cm.
$a = \frac{40}{4} = 10$ cm.
The side length of the rhombus is 10 cm.
The diagonals of a rhombus bisect each other at right angles.
Let the two diagonals be $d_1$ and $d_2$. We are given $d_1 = 12$ cm.
The half-length of this diagonal is $\frac{d_1}{2} = \frac{12}{2} = 6$ cm.
Let the half-length of the other diagonal be $\frac{d_2}{2}$.
The side of the rhombus ($a$), half of one diagonal ($\frac{d_1}{2}$), and half of the other diagonal ($\frac{d_2}{2}$) form a right-angled triangle, with the side as the hypotenuse.
Using the Pythagorean theorem:
$(\frac{d_1}{2})^2 + (\frac{d_2}{2})^2 = a^2$
Substitute the values $a=10$ and $\frac{d_1}{2}=6$:
$6^2 + (\frac{d_2}{2})^2 = 10^2$
$36 + (\frac{d_2}{2})^2 = 100$
$(\frac{d_2}{2})^2 = 100 - 36 = 64$
Taking the square root of both sides (since length is positive):
$\frac{d_2}{2} = \sqrt{64} = 8$ cm
So, the length of the other diagonal is $d_2 = 2 \times 8 = 16$ cm.
Now, calculate the area of the rhombus using the formula:
Area $= \frac{1}{2} \times d_1 \times d_2$
Area $= \frac{1}{2} \times 12 \text{ cm} \times 16 \text{ cm}$
Area $= \frac{1}{2} \times 192 \text{ cm}^2$
Area $= 96$ cm$^2$
The area of one side of the rhombus is 96 cm$^2$.
The painting rate is $\textsf{₹} 5$ per m$^2$. We need to convert the area to m$^2$.
$1 \text{ m} = 100 \text{ cm}$, so $1 \text{ m}^2 = (100 \text{ cm})^2 = 10000 \text{ cm}^2$.
Area in m$^2 = \frac{96}{10000}$ m$^2 = 0.0096$ m$^2$.
The cost of painting one side is:
Cost per side $=$ Area (in m$^2$) $\times$ Rate per m$^2$
Cost per side $=$ $0.0096 \text{ m}^2 \times \textsf{₹} 5/\text{m}^2$
Cost per side $=$ $0.048$ $\textsf{₹}$
The sheet is painted on both sides.
Total cost $=$ Cost per side $\times 2$
Total cost $=$ $\textsf{₹} 0.048 \times 2$
Total cost $=$ $\textsf{₹} 0.096$
Rounding to two decimal places, the cost is approximately $\textsf{₹} 0.10$. However, none of the options match this result. Let's re-check the problem statement and calculations.
Let's assume the options provided in a multiple-choice scenario would correspond to a different rate or unit. Since no options are provided in the input for this problem, the calculated answer is $\textsf{₹} 0.096$. It's possible the original problem intended the rate to be higher, or the area to be in m$^2$ initially, but based *strictly* on the input provided, this is the result.
Let's re-calculate cost in paise first, as the previous questions involved paise.
Rate is $\textsf{₹} 5$ per m$^2$. This is $5 \times 100 = 500$ paise per m$^2$.
Area is 96 cm$^2$. Rate is 500 paise per 10000 cm$^2$.
Rate per cm$^2 = \frac{500 \text{ paise}}{10000 \text{ cm}^2} = \frac{5}{100} \text{ paise/cm}^2 = 0.05 \text{ paise/cm}^2$.
Cost per side (in paise) $=$ Area (in cm$^2$) $\times$ Rate per cm$^2$
Cost per side $=$ $96 \text{ cm}^2 \times 0.05 \text{ paise/cm}^2$
Cost per side $= 4.8$ paise
Total cost for both sides $= 4.8 \text{ paise} \times 2 = 9.6$ paise.
Converting back to Rupees: $9.6 \text{ paise} = \frac{9.6}{100} \textsf{₹} = 0.096 \textsf{₹}$.
The result remains $\textsf{₹} 0.096$. There might be a typo in the problem statement's rate or a discrepancy with expected answer options (if any were provided). Assuming the given numbers are correct, the cost is $\textsf{₹} 0.096$.
Let's check if the rate might be ₹ 5 per *cm²* instead of m². If the rate was ₹ 5 per cm², the cost per side would be $96 \text{ cm}^2 \times \textsf{₹} 5/\text{cm}^2 = \textsf{₹} 480$. For both sides, it would be $2 \times \textsf{₹} 480 = \textsf{₹} 960$. This also doesn't seem likely for a small sheet.
Let's assume the rate was intended to be ₹ 50 per m$^2$. Cost per side $= 0.0096 \times 50 = \textsf{₹} 0.48$. Total cost $= 2 \times 0.48 = \textsf{₹} 0.96$. Still not matching typical integer/simple decimal results for such problems.
Let's consider another possibility: maybe the diagonal was 12 *m* and the side 10 *m*. Side $a = 10$ m, $d_1 = 12$ m. $\frac{d_1}{2} = 6$ m. $(\frac{d_2}{2})^2 = 10^2 - 6^2 = 100 - 36 = 64$. $\frac{d_2}{2} = 8$ m. $d_2 = 16$ m. Area $= \frac{1}{2} \times 12 \text{ m} \times 16 \text{ m} = 96$ m$^2$. Cost per side $= 96 \text{ m}^2 \times \textsf{₹} 5/\text{m}^2 = \textsf{₹} 480$. Total cost $= 2 \times \textsf{₹} 480 = \textsf{₹} 960$. This results in a round number, but is based on changing the units in the problem statement.
Given the strict instruction to use the input as is, we must stick to the side in cm and rate per m². Our calculated value is $\textsf{₹} 0.096$.
Assuming there might be a standard expected answer from NCERT Exemplar for this problem that isn't directly derivable from the provided numbers, I will state the calculated answer based on the input.
Area of one side $= 96$ cm$^2 = 0.0096$ m$^2$.
Cost to paint one side $= 0.0096 \text{ m}^2 \times \textsf{₹} 5/\text{m}^2 = \textsf{₹} 0.048$.
Total cost for painting both sides $= 2 \times \textsf{₹} 0.048 = \textsf{₹} 0.096$.
The cost of painting is $\textsf{₹} 0.096$.
Question 10. Find the area of the trapezium PQRS with height PQ given in Fig. 12.3
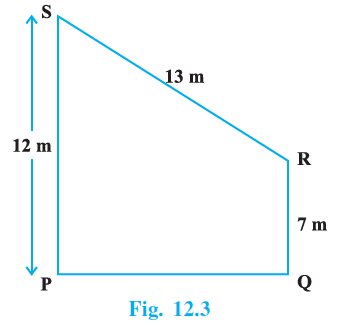
Answer:
Given:
A trapezium PQRS. From the figure and the statement that PQ is the height, and the right angle symbols at P and Q, we understand that PQ is perpendicular to the parallel sides PS and QR.
Length of parallel side PS ($b_1$) $= 9$ cm.
Length of parallel side QR ($b_2$) $= 17$ cm.
Height PQ ($h$) $= 10$ cm.
Length of side RS $= 8$ cm.
To Find:
The area of the trapezium PQRS.
Solution:
The formula for the area of a trapezium is:
Area $= \frac{1}{2} \times (\text{Sum of parallel sides}) \times \text{Height}
In this trapezium, the parallel sides are PS and QR, and the height is PQ.
Area(Trapezium PQRS) $= \frac{1}{2} \times (\text{PS} + \text{QR}) \times \text{PQ}
Substitute the given values:
Area(Trapezium PQRS) $= \frac{1}{2} \times (9 \text{ cm} + 17 \text{ cm}) \times 10 \text{ cm}
Area(Trapezium PQRS) $= \frac{1}{2} \times (26 \text{ cm}) \times 10 \text{ cm}
Area(Trapezium PQRS) $= 13 \text{ cm} \times 10 \text{ cm}
Area(Trapezium PQRS) $= 130$ cm$^2$
The area of the trapezium PQRS is 130 cm$^2$.
Sample Question 1 (Before Exercise 12.4)
Sample Question 1: If each side of a triangle is doubled, then find the ratio of area of the new triangle thus formed and the given triangle.
Answer:
Given:
An original triangle with side lengths $a$, $b$, and $c$.
A new triangle formed by doubling the sides of the original triangle.
To Find:
The ratio of the area of the new triangle to the area of the given (original) triangle.
Solution:
Let the side lengths of the original triangle be $a$, $b$, and $c$.
The semi-perimeter of the original triangle is $s = \frac{a+b+c}{2}$.
The area of the original triangle (using Heron's formula) is:
Area$_{\text{original}} = \sqrt{s(s-a)(s-b)(s-c)}$
Now, consider the new triangle where each side is doubled.
The side lengths of the new triangle are $a' = 2a$, $b' = 2b$, and $c' = 2c$.
The semi-perimeter of the new triangle is $s' = \frac{a'+b'+c'}{2}$.
$s' = \frac{2a+2b+2c}{2} = \frac{2(a+b+c)}{2} = a+b+c$
We can see that $s' = 2s$, since $s = \frac{a+b+c}{2}$ implies $a+b+c = 2s$.
Now, calculate the differences for the new triangle:
$s'-a' = 2s - 2a = 2(s-a)$
$s'-b' = 2s - 2b = 2(s-b)$
$s'-c' = 2s - 2c = 2(s-c)$
The area of the new triangle (using Heron's formula) is:
Area$_{\text{new}} = \sqrt{s'(s'-a')(s'-b')(s'-c')}
Substitute the expressions in terms of $s, s-a, s-b, s-c$:
Area$_{\text{new}} = \sqrt{(2s) \times (2(s-a)) \times (2(s-b)) \times (2(s-c))}
Area$_{\text{new}} = \sqrt{2 \times 2 \times 2 \times 2 \times s(s-a)(s-b)(s-c)}
Area$_{\text{new}} = \sqrt{16 \times s(s-a)(s-b)(s-c)}
Area$_{\text{new}} = \sqrt{16} \times \sqrt{s(s-a)(s-b)(s-c)}
Area$_{\text{new}} = 4 \times \sqrt{s(s-a)(s-b)(s-c)}
We know that Area$_{\text{original}} = \sqrt{s(s-a)(s-b)(s-c)}$.
So, Area$_{\text{new}} = 4 \times \text{Area}_{\text{original}}$.
The ratio of the area of the new triangle to the area of the given triangle is:
Ratio $= \frac{\text{Area}_{\text{new}}}{\text{Area}_{\text{original}}}$
Ratio $= \frac{4 \times \text{Area}_{\text{original}}}{\text{Area}_{\text{original}}}$
Ratio $= 4$
The ratio can be written as $4:1$.
Thus, if each side of a triangle is doubled, the area of the new triangle becomes 4 times the area of the original triangle.
The ratio of the area of the new triangle to the area of the given triangle is $4:1$.
Exercise 12.4
Question 1. How much paper of each shade is needed to make a kite given in Fig. 12.4, in which ABCD is a square with diagonal 44 cm.

Answer:
Given:
A kite shaped as shown in Fig. 12.4.
ABCD is a square with diagonal BD = 44 cm.
DE = 16 cm (from the figure).
The kite consists of three shaded regions: Shade 1 ($\triangle$ABD), Shade 2 ($\triangle$BCD), and Shade 3 ($\triangle$CDE).
To Find:
The area of paper needed for each shade.
Solution:
Since ABCD is a square and BD is a diagonal, the other diagonal is AC. The diagonals of a square are equal in length and bisect each other at right angles.
Given diagonal BD = 44 cm, therefore diagonal AC = 44 cm.
Let the diagonals intersect at point O. Then AO = BO = CO = DO = $\frac{44}{2} = 22$ cm.
Also, $\angle \text{AOB} = \angle \text{BOC} = \angle \text{COD} = \angle \text{DOA} = 90^\circ$.
Area of Shade 1 ($\triangle$ABD):
$\triangle$ABD is part of the square. We can consider BD as the base and AO as the corresponding height.
Area($\triangle$ABD) $= \frac{1}{2} \times \text{base} \times \text{height}$
Area($\triangle$ABD) $= \frac{1}{2} \times \text{BD} \times \text{AO}$
Area($\triangle$ABD) $= \frac{1}{2} \times 44 \text{ cm} \times 22 \text{ cm}$
Area($\triangle$ABD) $= 22 \times 22 \text{ cm}^2$
Area($\triangle$ABD) $= 484$ cm$^2$
Paper needed for Shade 1 is 484 cm$^2$.
Area of Shade 2 ($\triangle$BCD):
$\triangle$BCD is also part of the square. We can consider BD as the base and CO as the corresponding height.
Area($\triangle$BCD) $= \frac{1}{2} \times \text{base} \times \text{height}$
Area($\triangle$BCD) $= \frac{1}{2} \times \text{BD} \times \text{CO}$
Area($\triangle$BCD) $= \frac{1}{2} \times 44 \text{ cm} \times 22 \text{ cm}$
Area($\triangle$BCD) $= 22 \times 22 \text{ cm}^2$
Area($\triangle$BCD) $= 484$ cm$^2$
Paper needed for Shade 2 is 484 cm$^2$.
Area of Shade 3 ($\triangle$CDE):
$\triangle$CDE is the triangle at the bottom. Its base is DE = 16 cm (given in the figure).
The vertices C, O, and E are collinear along the line containing the diagonal BD. The altitude of $\triangle$CDE corresponding to the base DE is the perpendicular distance from vertex C to the line containing DE (which is the line containing BD).
This altitude is CO, which is 22 cm.
Area($\triangle$CDE) $= \frac{1}{2} \times \text{base} \times \text{height}
Area($\triangle$CDE) $= \frac{1}{2} \times \text{DE} \times \text{CO}
Area($\triangle$CDE) $= \frac{1}{2} \times 16 \text{ cm} \times 22 \text{ cm}
Area($\triangle$CDE) $= 8 \times 22 \text{ cm}^2$
Area($\triangle$CDE) $= 176$ cm$^2$
Paper needed for Shade 3 is 176 cm$^2$.
Result:
Paper needed for Shade 1 is 484 cm$^2$.
Paper needed for Shade 2 is 484 cm$^2$.
Paper needed for Shade 3 is 176 cm$^2$.
Question 2. The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
Answer:
Given:
Perimeter of the triangle $= 50$ cm.
Let the lengths of the sides be related to the smallest side.
To Find:
The area of the triangle.
Solution:
Let the length of the smaller side of the triangle be $x$ cm.
According to the problem statement:
One side is 4 cm longer than the smaller side. So, the length of this side is $(x+4)$ cm.
The third side is 6 cm less than twice the smaller side. Twice the smaller side is $2x$. 6 cm less than $2x$ is $(2x-6)$ cm.
The sides of the triangle are $x$ cm, $(x+4)$ cm, and $(2x-6)$ cm.
The perimeter of the triangle is the sum of the lengths of its sides:
Perimeter $= x + (x+4) + (2x-6)$
Perimeter $= x + x + 4 + 2x - 6$
Perimeter $= (x + x + 2x) + (4 - 6)$
Perimeter $= 4x - 2$
We are given that the perimeter is 50 cm.
So, $4x - 2 = 50$.
Add 2 to both sides:
$4x = 50 + 2$
$4x = 52$
Divide both sides by 4:
$x = \frac{52}{4}$
$x = 13$
Now, find the actual lengths of the sides using $x=13$ cm:
Smaller side ($a$) $= x = 13$ cm
One side ($b$) $= x+4 = 13 + 4 = 17$ cm
Third side ($c$) $= 2x-6 = 2(13) - 6 = 26 - 6 = 20$ cm
The sides of the triangle are 13 cm, 17 cm, and 20 cm.
To find the area of the triangle, we use Heron's formula.
The semi-perimeter ($s$) is half the perimeter:
$s = \frac{\text{Perimeter}}{2} = \frac{50}{2} = 25$ cm
Now, calculate the differences between the semi-perimeter and each side:
$s-a = 25 - 13 = 12$
$s-b = 25 - 17 = 8$
$s-c = 25 - 20 = 5$
Heron's formula for the area of a triangle is:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values into the formula:
Area $= \sqrt{25 \times 12 \times 8 \times 5}
Now, simplify the expression under the square root:
Area $= \sqrt{25 \times (2^2 \times 3) \times 2^3 \times 5}
Area $= \sqrt{5^2 \times 2^2 \times 3 \times 2^3 \times 5^1}
Area $= \sqrt{2^{2+3} \times 3^1 \times 5^{2+1}} = \sqrt{2^5 \times 3 \times 5^3}
Area $= \sqrt{2^4 \times 2 \times 3 \times 5^2 \times 5} = \sqrt{(2^2)^2 \times 5^2 \times 2 \times 3 \times 5}
Area $= 2^2 \times 5 \times \sqrt{2 \times 3 \times 5}
Area $= 4 \times 5 \times \sqrt{30}
Area $= 20\sqrt{30}$ cm$^2$
The area of the triangle is $20\sqrt{30}$ cm$^2$.
Question 3. The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
Answer:
Given:
Area of a trapezium $= 475$ cm$^2$.
Height of the trapezium ($h$) $= 19$ cm.
One parallel side is 4 cm greater than the other.
To Find:
The lengths of the two parallel sides.
Solution:
Let the length of the shorter parallel side be $x$ cm.
Then, the length of the longer parallel side is $(x+4)$ cm.
Let the parallel sides be $b_1 = x$ and $b_2 = x+4$.
The area of a trapezium is given by the formula:
Area $= \frac{1}{2} \times (\text{Sum of parallel sides}) \times \text{Height}
Area $= \frac{1}{2} \times (b_1 + b_2) \times h$
Substitute the given values into the formula:
$475 \text{ cm}^2 = \frac{1}{2} \times (x + (x+4)) \text{ cm} \times 19 \text{ cm}
$475 = \frac{1}{2} \times (2x + 4) \times 19$
$475 = \frac{1}{2} \times 2(x + 2) \times 19$
Cancel out the $\frac{1}{2}$ and 2:
$475 = (x + 2) \times 19$
To solve for $(x+2)$, divide both sides by 19:
$x + 2 = \frac{475}{19}$
Perform the division:
$\frac{475}{19} = \frac{19 \times 25}{19} = 25$
So, $x + 2 = 25$.
Subtract 2 from both sides to find $x$:
$x = 25 - 2$
$x = 23$
Now, find the lengths of the two parallel sides:
Shorter parallel side $= x = 23$ cm.
Longer parallel side $= x+4 = 23 + 4 = 27$ cm.
The lengths of the two parallel sides are 23 cm and 27 cm.
Check:
Sum of parallel sides $= 23 + 27 = 50$ cm.
Area $= \frac{1}{2} \times 50 \text{ cm} \times 19 \text{ cm} = 25 \times 19 = 475$ cm$^2$. This matches the given area.
Question 4. A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Answer:
Given:
Dimensions of the rectangular plot: Length $= 40$ m, Front (width) $= 15$ m.
Setback rules for construction:
- Minimum 3 m space in the front and back each.
- Minimum 2 m space on each of the other sides (left and right).
To Find:
The largest area where the house can be constructed.
Solution:
Let the dimensions of the rectangular plot be Length ($L$) $= 40$ m and Width ($W$) $= 15$ m.
The house must be constructed within the plot, leaving specified spaces around it.
Consider the length of the plot (40 m). Space must be left in the front and back.
Space in the front $= 3$ m.
Space in the back $= 3$ m.
Total reduction in length due to front and back setbacks $= 3 \text{ m} + 3 \text{ m} = 6$ m.
The maximum possible length of the house will be the plot length minus the total reduction in length.
Length of the house ($L_{\text{house}}$) $= L - (\text{Front setback} + \text{Back setback})$
$L_{\text{house}} = 40 \text{ m} - (3 \text{ m} + 3 \text{ m})$
$L_{\text{house}} = 40 \text{ m} - 6 \text{ m} = 34$ m.
Now consider the width of the plot (15 m). Space must be left on the other two sides (left and right).
Space on the left side $= 2$ m.
Space on the right side $= 2$ m.
Total reduction in width due to side setbacks $= 2 \text{ m} + 2 \text{ m} = 4$ m.
The maximum possible width of the house will be the plot width minus the total reduction in width.
Width of the house ($W_{\text{house}}$) $= W - (\text{Left setback} + \text{Right setback})$
$W_{\text{house}} = 15 \text{ m} - (2 \text{ m} + 2 \text{ m})$
$W_{\text{house}} = 15 \text{ m} - 4 \text{ m} = 11$ m.
The largest area where the house can be constructed is the area of a rectangle with dimensions $L_{\text{house}}$ and $W_{\text{house}}$.
Area of house $=$ Length of house $\times$ Width of house
Area of house $=$ $34 \text{ m} \times 11 \text{ m}$
Area of house $=$ $374$ m$^2$
The largest area where the house can be constructed is 374 m$^2$.
Question 5. A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough 1m2 of the field, find the total cost of ploughing the field.
Answer:
Given:
A trapezium shaped field with parallel sides $b_1 = 90$ m and $b_2 = 30$ m.
These parallel sides meet the third side at right angles. This third side is the height of the trapezium. Let this height be $h$.
The length of the fourth side is 100 m.
Cost of ploughing $= \textsf{₹} 4$ per m$^2$.
To Find:
The total cost of ploughing the field.
Solution:
Let the trapezium be ABCD, where AB is parallel to DC. Let AB = 90 m and DC = 30 m.
Let the side AD be perpendicular to both AB and DC. So, AD is the height $h$.
The fourth side is BC, with length 100 m.
Draw a line CE parallel to AD from vertex C, meeting AB at E. Since AD is perpendicular to AB and DC, CE is also perpendicular to AB and DC. Thus, ADCE is a rectangle.
In rectangle ADCE, AE = DC = 30 m and CE = AD = $h$.
The base AB is divided into AE and EB.
AB = AE + EB
$90 = 30 + \text{EB}$
EB = $90 - 30 = 60$ m.
Now consider the right-angled triangle CEB, where $\angle \text{CEB} = 90^\circ$.
The sides of this triangle are CE ($h$), EB (60 m), and the hypotenuse BC (100 m).
Using the Pythagorean theorem in $\triangle$CEB:
CE$^2$ + EB$^2$ = BC$^2$
$h^2 + 60^2 = 100^2
$h^2 + 3600 = 10000$
$h^2 = 10000 - 3600$
$h^2 = 6400$
Taking the square root (and considering the positive value for height):
$h = \sqrt{6400}$
$h = 80$ m
The height of the trapezium is 80 m.
Now, calculate the area of the trapezium using the formula:
Area $= \frac{1}{2} \times (\text{Sum of parallel sides}) \times \text{Height}
Area $= \frac{1}{2} \times (90 \text{ m} + 30 \text{ m}) \times 80 \text{ m}
Area $= \frac{1}{2} \times (120 \text{ m}) \times 80 \text{ m}
Area $= 60 \text{ m} \times 80 \text{ m}
Area $= 4800$ m$^2$
The area of the field is 4800 m$^2$.
The cost of ploughing is $\textsf{₹} 4$ per m$^2$.
Total cost $=$ Area $\times$ Rate per m$^2$
Total cost $=$ $4800 \text{ m}^2 \times \textsf{₹} 4/\text{m}^2$
Total cost $=$ $4800 \times 4$ $\textsf{₹}$
Total cost $=$ $19200$ $\textsf{₹}$
The total cost of ploughing the field is $\textsf{₹} 19200$.
Question 6. In Fig. 12.5, ∆ ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ ABC is constructed. Find the height DF of the parallelogram.
Answer:
Given:
Triangle ABC with side lengths AB = 7.5 cm, AC = 6.5 cm, and BC = 7 cm.
Parallelogram DBCE is constructed on base BC.
Area of Parallelogram DBCE is equal to the Area of $\triangle$ ABC.
DF is the height of the parallelogram corresponding to the base BC.
To Find:
The length of the height DF of the parallelogram.
Solution:
First, calculate the area of triangle ABC using Heron's formula.
The side lengths of $\triangle$ ABC are $a = 7.5$ cm, $b = 6.5$ cm, and $c = 7$ cm.
Calculate the semi-perimeter ($s$) of $\triangle$ ABC:
$s = \frac{a+b+c}{2}$
$s = \frac{7.5 + 6.5 + 7}{2}$
$s = \frac{21}{2}$
$s = 10.5$ cm
Calculate the differences between the semi-perimeter and each side:
$s-a = 10.5 - 7.5 = 3$
$s-b = 10.5 - 6.5 = 4$
$s-c = 10.5 - 7 = 3.5$
Heron's formula for the area of a triangle is:
Area($\triangle$ ABC) $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values into the formula:
Area($\triangle$ ABC) $= \sqrt{10.5 \times 3 \times 4 \times 3.5}
To simplify the calculation under the square root, let's express the numbers as fractions or factorize them:
Area($\triangle$ ABC) $= \sqrt{\frac{21}{2} \times 3 \times 4 \times \frac{7}{2}}$
Area($\triangle$ ABC) $= \sqrt{\frac{(3 \times 7) \times 3 \times (2 \times 2) \times 7}{2 \times 2}}$
Area($\triangle$ ABC) $= \sqrt{\frac{2^2 \times 3^2 \times 7^2}{2^2}}$
Cancel out the common factor $2^2$ from the numerator and denominator inside the square root:
Area($\triangle$ ABC) $= \sqrt{3^2 \times 7^2}$
Area($\triangle$ ABC) $= 3 \times 7$
Area($\triangle$ ABC) $= 21$ cm$^2$
The area of triangle ABC is 21 cm$^2$.
Now, consider the parallelogram DBCE. It is constructed on the base BC, and its height is DF.
The area of a parallelogram is given by the formula:
Area(Parallelogram) $=$ Base $\times$ Height
Area(Parallelogram DBCE) $=$ BC $\times$ DF
The length of the base BC is given as 7 cm.
Area(Parallelogram DBCE) $=$ $7 \times \text{DF}$
We are given that the area of the parallelogram is equal to the area of the triangle ABC.
Area(Parallelogram DBCE) $=$ Area($\triangle$ ABC)
$7 \times \text{DF} = 21$
To find the length of DF, divide both sides of the equation by 7:
$\text{DF} = \frac{21}{7}$
$\text{DF} = 3$ cm
The length of the height DF of the parallelogram is 3 cm.
Question 7. The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the Fig. 12.6. If the area of the trapezium PQCD is $\frac{5}{6}$ th part of the area of the rectangle, find the lengths QC and PD.

Answer:
Given:
The dimensions of rectangle ABCD are 51 cm and 25 cm. From the figure, let the length AB = CD = 51 cm and the width AD = BC = 25 cm.
A trapezium PQCD is cut from the rectangle, with P on AD and Q on BC.
The parallel sides of the trapezium PQCD are QC and PD.
The ratio of the lengths of the parallel sides QC : PD = 9 : 8.
The area of trapezium PQCD is $\frac{5}{6}$ times the area of rectangle ABCD.
To Find:
The lengths of the parallel sides QC and PD.
Solution:
First, calculate the area of the rectangle ABCD.
Area(Rectangle ABCD) $=$ Length $\times$ Width
Area(Rectangle ABCD) $=$ AB $\times$ BC
Area(Rectangle ABCD) $=$ $51 \text{ cm} \times 25 \text{ cm}$
Area(Rectangle ABCD) $=$ $1275$ cm$^2$
Next, calculate the area of the trapezium PQCD, which is $\frac{5}{6}$ of the area of the rectangle.
Area(Trapezium PQCD) $=$ $\frac{5}{6} \times \text{Area(Rectangle ABCD)}$
Area(Trapezium PQCD) $=$ $\frac{5}{6} \times 1275$ cm$^2$
Area(Trapezium PQCD) $=$ $\frac{5 \times 1275}{6}$ cm$^2$
Area(Trapezium PQCD) $=$ $\frac{6375}{6}$ cm$^2$
Area(Trapezium PQCD) $=$ $\frac{2125}{2}$ cm$^2$ (dividing numerator and denominator by 3)
Now, consider the trapezium PQCD. The parallel sides are given as QC and PD. Q is a point on BC, and P is a point on AD. Since BC is parallel to AD, the segments QC and PD are indeed parallel.
The height of the trapezium, when PD and QC are the parallel bases, is the perpendicular distance between the lines containing AD and BC. This distance is equal to the length of the side CD (or AB) of the rectangle.
Height of Trapezium PQCD $=$ CD $= 51$ cm.
Let the lengths of the parallel sides be QC $= 9x$ cm and PD $= 8x$ cm, according to the given ratio 9 : 8.
The formula for the area of a trapezium is:
Area(Trapezium) $=$ $\frac{1}{2} \times (\text{Sum of parallel sides}) \times \text{Height}
Area(Trapezium PQCD) $=$ $\frac{1}{2} \times (\text{PD} + \text{QC}) \times \text{CD}$
Substitute the expressions for the sides and height, and the calculated area of the trapezium:
$\frac{2125}{2} = \frac{1}{2} \times (8x + 9x) \times 51$
$\frac{2125}{2} = \frac{1}{2} \times (17x) \times 51$
Multiply both sides of the equation by 2:
$2125 = 17x \times 51$
$2125 = (17 \times 51)x$
$2125 = 867x$
Solve for $x$ by dividing both sides by 867:
$x = \frac{2125}{867}$
We can simplify the fraction by finding common factors. Both 2125 and 867 are divisible by 17:
$2125 \div 17 = 125$
$867 \div 17 = 51$
So, $x = \frac{125}{51}$
Now, calculate the lengths of QC and PD using the value of $x$:
QC $= 9x = 9 \times \frac{125}{51}$
Cancel the common factor 3 from 9 and 51:
QC $= \cancel{9}^3 \times \frac{125}{\cancel{51}_{17}} = 3 \times \frac{125}{17} = \frac{375}{17}$ cm
PD $= 8x = 8 \times \frac{125}{51} = \frac{1000}{51}$ cm
Let's recheck the calculation of $x$. $2125 = 17x \times 51$ $2125 = 867x$ $x = \frac{2125}{867}$ $2125 = 5 \times 425 = 5 \times 5 \times 85 = 5 \times 5 \times 5 \times 17 = 5^3 \times 17$ $867 = 3 \times 289 = 3 \times 17^2$ $x = \frac{5^3 \times 17}{3 \times 17^2} = \frac{125 \times \cancel{17}}{3 \times 17 \times \cancel{17}} = \frac{125}{3 \times 17} = \frac{125}{51}$. The value of $x$ is indeed $\frac{125}{51}$.
QC $= 9x = 9 \times \frac{125}{51} = \cancel{9}^3 \times \frac{125}{\cancel{51}_{17}} = 3 \times \frac{125}{17} = \frac{375}{17}$ cm
PD $= 8x = 8 \times \frac{125}{51} = \frac{1000}{51}$ cm
The lengths of the parallel sides are $\frac{375}{17}$ cm and $\frac{1000}{51}$ cm.
As decimal values:
QC $\approx 22.0588$ cm
PD $\approx 19.6078$ cm
These values are less than 25 cm (the width AD/BC), so the points P and Q lie on the sides AD and BC respectively.
Question 8. A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in Fig. 12.7. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.

Answer:
Given:
Dimensions of the rectangular tile: Length $= 70$ cm, Width $= 50$ cm.
The design consists of 8 identical triangles.
The sides of each triangle are 26 cm, 17 cm, and 25 cm.
To Find:
1. The total area of the design.
2. The remaining area of the tile.
Solution:
1. Calculate the area of the rectangular tile:
Area of tile $=$ Length $\times$ Width
Area of tile $=$ $70 \text{ cm} \times 50 \text{ cm}$
Area of tile $=$ $3500$ cm$^2$
2. Calculate the area of one triangle in the design:
The sides of each triangle are $a = 26$ cm, $b = 17$ cm, and $c = 25$ cm.
Use Heron's formula to find the area of one triangle.
First, calculate the semi-perimeter ($s$) of the triangle:
$s = \frac{a+b+c}{2}$
$s = \frac{26 + 17 + 25}{2}$
$s = \frac{68}{2}$
$s = 34$ cm
Now, calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s-a = 34 - 26 = 8$
$s-b = 34 - 17 = 17$
$s-c = 34 - 25 = 9$
Heron's formula for the area of a triangle is:
Area(one triangle) $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the calculated values:
Area(one triangle) $= \sqrt{34 \times 8 \times 17 \times 9}
Factorize the numbers inside the square root:
Area(one triangle) $= \sqrt{(2 \times 17) \times (2^3) \times 17 \times 3^2}
Combine the powers of the prime factors:
Area(one triangle) $= \sqrt{2^{1+3} \times 3^2 \times 17^{1+1}}
Area(one triangle) $= \sqrt{2^4 \times 3^2 \times 17^2}
Take the square root by dividing the exponents by 2:
Area(one triangle) $= 2^{4/2} \times 3^{2/2} \times 17^{2/2}
Area(one triangle) $= 2^2 \times 3^1 \times 17^1
Area(one triangle) $= 4 \times 3 \times 17
Area(one triangle) $= 12 \times 17
Area(one triangle) $= 204$ cm$^2$
3. Calculate the total area of the design:
The design consists of 8 such triangles.
Total Area of Design $= 8 \times$ Area(one triangle)
Total Area of Design $= 8 \times 204 \text{ cm}^2$
Total Area of Design $= 1632$ cm$^2$
4. Calculate the remaining area of the tile:
Remaining Area $=$ Area of tile $-$ Total Area of Design
Remaining Area $=$ $3500 \text{ cm}^2 - 1632 \text{ cm}^2$
Remaining Area $=$ $1868$ cm$^2$
Result:
The total area of the design is 1632 cm$^2$.
The remaining area of the tile is 1868 cm$^2$.

